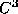Kai T. Hansen
We will here review and criticise some arguments given in
ref. [KKY] by Kan, Koçak, and Yorke. The main result in [KKY] is the antimonotonicity theorem stating the following:
In any neighborhood of a nondegenerate, homoclinic-tangency
parameter value of a one-parameter family of dissipative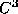 
diffeomorphisms of the plane, there must be both infinitely many
orbit-creation and infinitely many orbit-annihilation parameter
values.
We agree with [KKY] that there will exist some one-parameter families with both orbit-creations and orbit-annihilations, but we do not agree that all one-parameter families must have this property. We believe that there will exist cones in a high dimensional parameter space which include one-parameter families where orbits are only created as the parameter increases. We will analyse here the arguments in [KKY], and conclude that the arguments used here are not sufficient to claim that all one-parameter families are antimonotone.
The authors of [KKY] use a relatively simple example to illustrate their arguments. The proof for the general case follows the same type of arguments as the specific example, so the argument that we find to fail in the specific case should also invalidate the proof of the general case. We will therefore discuss only the specific example given by Kan et al.
The model given in [KKY] is the map
The regions A, C, and B are given by 
,
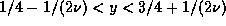, and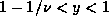 
respectively. We
assume here that the border for region C should be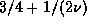 
rather than 
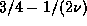as written in ref. [KKY]. This
modification makes the map symmetric, but is otherwise unimportant for
the arguments to follow. The number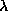 
is the parameter of the
map while 
and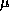 
are fixed numbers fulfilling 
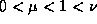and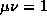 
. The figures shown here were evaluated with 
.
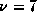Regardless of the value of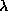 
this map will have one complete
Cantor set of non-wandering orbits denoted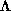 
. In addition
there exist families of non-wandering orbits which are created or
destroyed as the parameter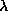 
is varied. The question raised
in [KKY] is whether non-wandering orbits will be both created and
destroyed as 
increases, especially for small negative values
of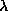 
. The authors construct an example, discussed below, which
is used to argue that there will be destroyed orbits as
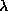increases. We find this argument not valid.
Figure 1 (a) shows the three regions A, C, and
B. Figure 1 (b) shows the mapping of these regions.
A part of the unstable and stable manifolds of the fixed point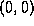 
are drawn in figure 2. The set 
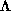is the
closure of the crossings between the parts of the stable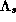 
and unstable 
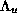manifolds of 
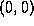which never leave the
regions A and B. These manifolds are horizontal and vertical
lines, not changing with changing parameter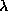 
, and they can be
labelled using a binary symbolic dynamics, given by the order in which
the trajectory visits the regions A and B.
The image of one vertical line of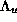 
through the region
C is a parabola with a minimum point at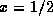 
. This parabola
is in [KKY] denoted a primary unstable line segment
and is parametrised as
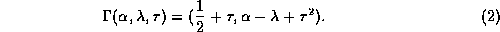
Here 
is a negative number corresponding to one point in
the Cantor set of unstable manifolds, that is
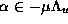. We remark here that 
is not a
function o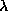f 
. If 
depends on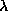 
then
this parabola is a part of the unstable manifold only for a
specific parameter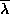 
and not for all
parameters close to this, since close to any point in a
Cantor set there will be an open gap.
Kan et al. choose to look at the case where the center part of the primary unstable parabola is mapped n times in region A and then enters the region C where the image of the parabola is a new narrow parabola
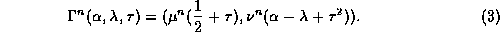
If the minimum point of this parabola is larger than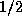 
then the
next image of this fold is in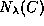 
and has one minimum
point close to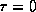 
. If the minimum point of
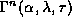is less than 
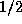and not too close
to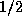 
then the image of the parabola has one maximum point close to
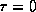and two minimum points.
The image of the narrow parabola is
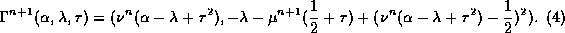
The partial derivative of the y coordinate with respect to
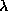is then found to be
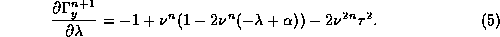
We find that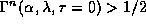 
if and only if
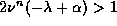and therefore have that
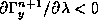. This implies that as
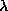increases the minimum point decreases and new homoclinic
orbits may be created. The minimum point
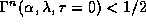if and only if
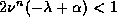. Since 
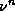is a large number we
will have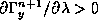 
unless the
minimum point is very close to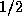 
or 
is very different from
zero. We then find that the maximum point increases with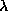 
and can create new homoclinic orbits. The primary parabola with a
minimum point goes downward with an increasing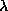 
and also
gives the possibility of creating new orbits without destroying any
other orbits. The conclusion here is that all the manifolds discussed
here only create and do not destroy orbits as 
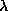increases.
This is illustrated in figure 2 where the manifolds
move in this way.
This conclusion is the opposite of the conclusion in ref. [KKY],
because the authors there do not consider parabolas with a fixed
value of 
but let 
be a function of 
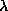. With
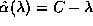where C depends on 
, 
,
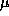and n, they find that one obtains a curve
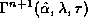with a maximum point that
decreases with increasing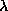 
. As we increase 
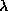two
crossing points between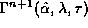 
and
a horizontal line belonging to the stable manifolds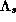 
will
disappear in a point where the curves are tangents. The authors use
density arguments to show that there will exist a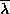 
such that this tangency point is a homoclinic tangency between a
stable and unstable manifold. We agree that if
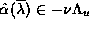then the tangency is a homoclinic tangency, but
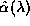for any 
is not
guaranteed to be in the unstable manifold and especially will it not
be the same fold as specified by e.g. a symbolic alphabet since the
folds are fixed on the x-axis under changes of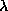 
. How the
crossings between the curve given by 
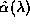and a
horizontal stable manifold change, tells us nothing about which orbits
that are created in the non-wandering set. The authors claim that
this proves that orbits are destroyed is therefore not valid. The
homoclinic tangencies are for this example in fact contact-creating
and not contact breaking as claimed in ref. [KKY].
We conclude that the Antimonotonicity theorem is not proven.
We have not succeeded in disproving the theorem, but believe that it is wrong as stated. In general one can presumably associate a parameter with the height of every primary unstable parabola, thus having a parameter space of an infinite, uncountable dimension. This parameter space set could be well approximated with a finite number of parameters if the manifolds form a not too dense Cantor set. We have done this [Han,HC] for the Hénon map where we have used symbolic dynamics to construct an approximate parameter space (assuming the existence of a symbolic dynamics for the maps of Hénon type). Bifurcation planes can be analytically found in this parameter space and there exist a large cone from every parameter point in which all one-dimensional parameter paths are monotone. These results are confirmed by numerics for the Hénon map. One observes non-monotonicity if one chooses a parameter path which is not inside a proper cone in the parameter space. Most one-dimensional parameter paths in a high dimensional parameter space will not be in a proper cone and one can therefore in numerical experiments expect to see both bifurcations and inverse bifurcations.
