An impact oscillator is a system that has some forcing potential
driving a particle to repeatedly impact a barrier. The impact oscillator
has long been an interesting system of study for both engineers and
physicists. For engineers it acts as a nice model of systems such as
earthquake scenarios [1], articulated mooring towers [2], and engine
rattling [3].  Fermi investigated the same system when dealing with cosmic
rays impacting the atmosphere [4].  This system is also ideal for studying
the dynamics of a seemingly chaotic system.  It’s conceptually easy to
grasp, yet there is still much to learn about it.
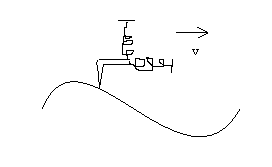
        One particular generalization of the impact oscillator is to
consider a particle bouncing on a two dimensional, infinitely long,
infinitely dense table with some known periodic curvature.  The particle
is being pulled along at some velocity, v, and the forcing potential is due
to a combination of a vertical and horizontal spring acting on the particle.
The ball has some coefficient of restitution that does not conserve energy
at the impact.  There is also a kinetic friction term that will resist the
motion of the ball on the surface. One particular physical interpretation
would be an atomic force microscope being drug along a surface at some
velocity v.

        The goal of this project is to study the dynamics of this system.
It is believed that at certain velocities, the particle will bounce
chaotically along the surface.  This project will include an investigation
of what velocities the chaotic bouncing will occur, both theoretically and
numerically by using tools such as bifurcation diagrams with the varied
parameter being velocity.  This system will be recast into a billiard system
and will then readily admit a 3-dimensional Jacobian and also giving a
3-dimensional Poincare’ map.  This project will also include an investigation
of the system using periodic orbit theory. A few additional things that we
will play with is using a Lorentz map of the maximum height the ball reaches
relative to the surface verses the previous maximum height. We will also
investigate using the technique of the PIM-triple method [5].  
	The ultimate, and therefore ideal, goal of this project is then to
understand this system well enough to make a prediction of the coefficient
of kinetic friction just by knowing when the ball begins to bounce chaotically.

[1]  J. M. T. Thompson and R. Ghaffari. Phys. Lett. A 91 5 (1982)
[2]  J.M.T. Thompson, A.R. Bokaian & R. Ghaffari. J. Energy Resources Technology (Trans ASME), 106, 191-198 (1984).
[3]  S. W. Shaw and P. J. Holmes.  Phys Rev Lett 51 623 (1983)
[4]  E. Fermi. Phys. Rev. 75, 1169 (1949)
[5]  H. E. Nusse and J. A. Yorke. Physica D 36, 137 (1989).